[Deep Learning] IoU 개념 정리 (IoU, GIoU, DIoU, CIoU)

요약

•   IoU: 교집합 / 합집합
•   GIoU: 두 박스를 모두 포함하는 최소 영역인 C 박스 활용
•   DIoU: IoU와 중심점 좌표 함께 고려
•   CIoU: DIoU와 geometric measure 함께 고려

---

 

1. IoU (Intersection over Union)

IoU란 Intersection over Union로 Object Detection 분야에서 예측 Bounding Box와 Ground Truth가 일치하는 정도를 0과 1 사이의 값으로 나타낸 값이다.

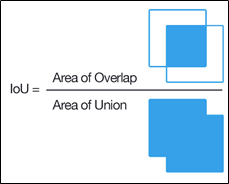
IoU는 두 box 영역의 (교집합) / (합집합) 을 의미

 

@ Object Detection Loss function에서 IoU의 필요성

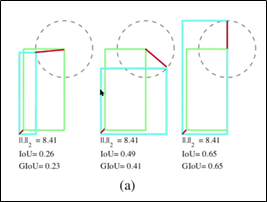
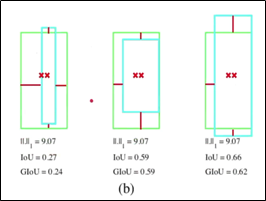
위의 그림 (a)에서 볼 수 있듯이 두 박스의 왼쪽 하단 거리와 오른쪽 상단 거리가 동일할 때, MSE (=L2 loss)는 일정하지만 box의 겹침 정도를 나타내는 IoU는 값이 변한다. 동일하게 그림 (b)에서도 중심 사이의 거리와 높이, 너비 차이가 동일할 때, L1 loss는 일정하지만, IoU는 값이 변한다.

   ▷▶ Object Detection에서 단순히 box의 좌표 차이를 통해 loss를 구하는 것보다 IoU를 loss에 활용하는 것이 regression loss에 더 적합할 수 있음을 알 수 있다.

 

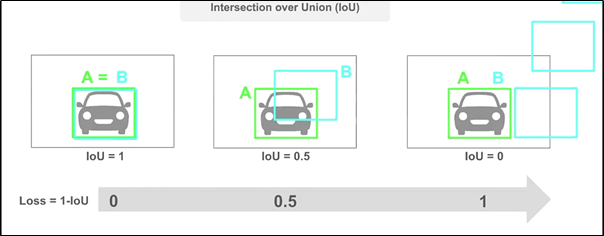
Loss = 1 - IoU

Object detection에서 1 - IoU 를 loss로 사용하는 경우

위 그림의 세 번째 예시처럼 두 박스가 겹치지 않을 경우 어느 정도의 오차로 교집합이 생기지 않은 것인지 알 수 없어 gradient vanishing 문제가 발생한다.

   ▷▶ 이러한 문제를 해결하기 위해 등장한 방법이 GIoU 이다.

 

2. GIoU (Generalized-IoU)

Generalized Intersection over Union: A Metric and A Loss for Bounding Box Regression 논문에서 제안된 방법으로 Bbox와 GT를 모두 포함하는 최소 크기의 C 박스를 활용한다. https://arxiv.org/abs/1902.09630

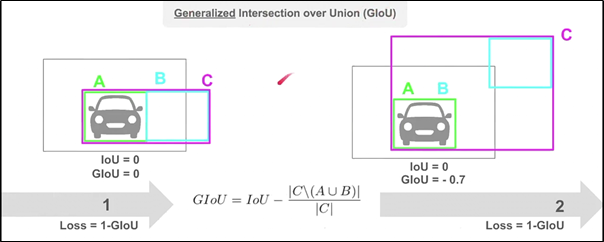
GIoU

C box는 A와 B box를 포함하는 가장 작은 box이고, C＼(A ∪ B)는 C box 영역에서 A와 B box의 합집합을 뺀 영역을 의미한다.

기존 IoU의 값에서 C box 중 A와 B 모두와 겹치지 않는 영역의 비율을 뺀 값이 GIoU가 된다. (GIoU가 클수록 좋음)

• 왼쪽 예시는     IoU=0, C＼(A ∪ B) = 0      →     GIoU=0
• 오른쪽 예시는  IoU=0, C＼(A ∪ B) = 0.7    →     GIoU=-0.7

 

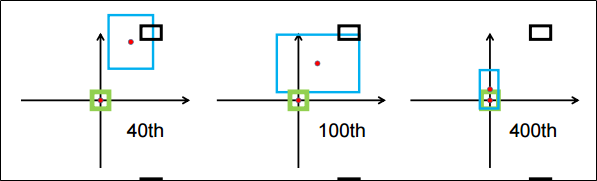
GIoU Loss를 활용한 Bbox 예측 과정

Object detection에서 1 - GIoU를 loss로 사용하는 경우 

(Loss 값의 범위는 0~2)

Iteration에 따른 GIoU Loss의 bounding box 예측 과정(초록: GT, 파랑: Bbox)을 보면 GT와의 overlap을 위해 Bbox 영역이 넓어지고, overlap 된 후 IoU를 높이기 위해 Bbox 영역 줄이는 방식으로 수행된다. 

이를 통해 겹치지 않는 박스에 대한 gradient vanishing 문제는 개선했지만 수렴 속도가 느리고 부정확하게 (horizontal과 vertical 정보 표현 X) 박스를 예측한다는 문제점 존재한다.

   ▷▶ 이러한 문제를 해결하기 위해 등장한 방법이DIoU이다.

 

3. DIoU (Distance-IoU)

Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression 논문에서 제안된 방법으로 IoU와 함께 중심 좌표를 활용한다. https://arxiv.org/pdf/1911.08287.pdf

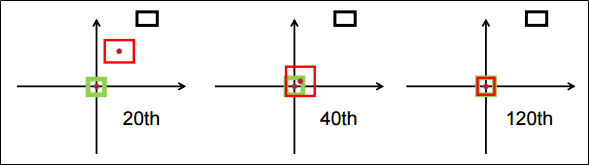
DIoU Loss를 활용한 Bbox 예측 과정

Iteration에 따른 DIoU Loss의 bounding box 예측 과정(초록: GT, 빨강: Bbox)을 보면 GT와의 overlap을 위해 Bbox 영역을 넓히는 GIoU와는 달리 DIoU는 중심 좌표를 비교하여 Bbox 자체가 GT 쪽으로 이동하는 것을 확인할 수 있다.

 

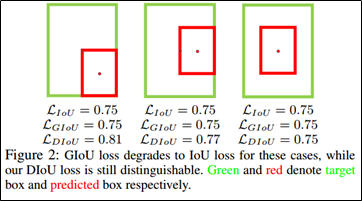
동일한 정도가 겹쳤을 때 IoU, GIoU, DIoU Loss 비교 결과

두 box가 겹쳐진 영역의 크기가 동일하고 Bbox의 위치만 달라졌을 경우, IoU, GIoU는 Bbox의 위치를 고려하지 않아 Loss값이 변하지 않지만, 중심 좌표를 활용하는 DIoU는 해당 좌표가 변함에 따라 Loss 값도 변하는 것을 확인할 수 있다.

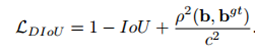
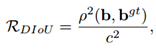
L(DIoU)는 기존 IoU Loss에 중심 좌표를 고려하는 수식을 추가한 수식으로, ρ는 Euclidean distance, b는 Bbox, b^gt는 GT의 중심 좌표, c는 Bbox와 GT를 포함하는 최소 박스인 C 박스의 대각 길이를 의미한다.

 

Object detection에서 DIoU Loss를 loss로 사용하는 경우

두 box가 겹치지 않았을 때, GIoU처럼 Bbox의 영역을 넓히지 않고 중심 좌표를 통해 박스의 거리 차이를 최소화 함으로써 수렴 속도를 향상시켰다.

 

@ DIoU를 NMS에 적용 시 위 그림처럼 동일한 class의 GT가 여러 개 겹쳐져 있는 경우 IoU에 비해 robust 한 것을 확인할 수 있다.

 

4. CIoU (Complete-IoU)

DIoU가 제안되었던 Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression 논문에서 동시에 제안된 방법으로 저자는 Bbox에 대한 좋은 Loss는 overlap area, central point distance, aspect ratio 세 요소를 고려하는 것이라고 말한다. 따라서 overlap area와 central point distance를 고려하는 DIoU에 추가적으로 aspect ratio를 고려하는 CIoU를 제안한다.

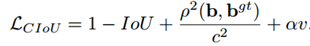
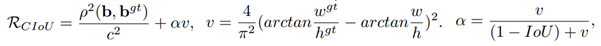
이때, v는 두 box의 aspect ration (종횡비)의 일치성을 측정하는 역할이고, α는 positive trade-off parameter로 non-overlapping case와 overlapping case의 균형을 조절하는 역할을 한다. 특히 non-overlapping 경우에 overlap area factor가 regression loss에 더 높은 우선순위를 갖게 한다.